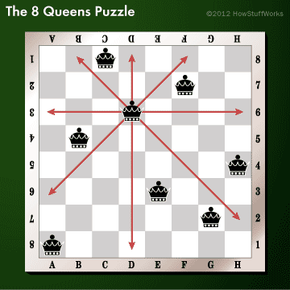
根据圆你运行在说什么,你最好的朋友是一个电脑程序员和你妹妹是一个象棋神童——您可能已经熟悉8皇后区难题。对于我们其余的人来说,八皇后拼图(或问题或简单的“八皇后”)可能不是我们花了很多时间思考。
谜题很简单。18新利最新登入你怎么能把八皇后棋盘,没有两个互相攻击吗?交替,问题是有时表示为“皇后区的最大数量,可以放在棋盘上,所以没有两个可以互相攻击,“但是当你这个谜题变得少了很多困难谷歌,“八皇后拼图”一词。
广告
你也许会问自己,为什么地球上的任何人都在乎,你保持你的八皇后。是的,从表面上看,它只是一个战略问题。但是(这就是它方便的代码有一个最好的朋友电脑)8皇后区拼图是一个伟大的方法来测试一个程序员的头脑和素养。
现在,不要害怕。你将不会被迫理解错综复杂的计算机编程来继续阅读。但是你应该知道解决这个问题可以通过使用一个程序代码,有些人比其他人更优雅。例如,您一定可以找到解决方案使用“暴力”程序,可能只是经历每一个可能的位置,排除一次。而是一个复杂的编码器将能够构建一个程序快捷键使用一个更雅致算法找你解决方案更快。能够想出不寻常或原始代码解决一个问题的方法广泛的八皇后可以成为一个伟大的测试code-writer的精明。
因此,尽管我们不会骗1和0你解释8王后是如何工作的,我们会给你一些解决难题。18新利最新登入
广告