分形
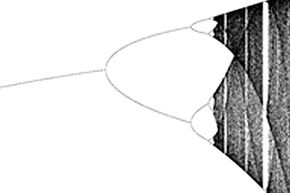
如果你仔细检查分岔图,你开始看到有趣的模式。例如,首先完成图,如第一张图片。
接下来,第一翻倍放大点。它看起来像一个圆形,侧面诉现在看看较小,侧向V的,下一个系列的。
广告
现在再次放大,说,高层,小V。
注意到这个区域18新利最新登入的图看起来像原来的。换句话说,这个数字是重复多次的大型结构。翻倍区域表现出一种被称为质量自相似性——像大的小区域。即使你看起来混乱的地区的图(向右发生),你可以找到这种品质。
自相似性是几何对象的一个类的属性称为分形。波兰数学家Benoit Mandelbrot在1975年创造了这个词,拉丁词碎云的,这意味着“破碎的”或“支离破碎”。He also worked out the basic math of the objects and described their properties. In addition to self-similarity, fractals also possess something known as分形维数衡量他们的复杂性。维数不是整数,1,2,3,但一小部分。例如,一个分形线1和2之间的一个维度。
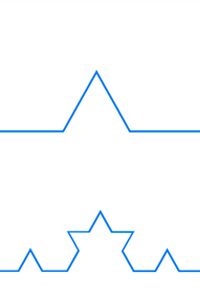
的科赫雪花——瑞典数学家命名的赫尔格·范·科赫站作为分形的一个典型的例子。推导出形状,范·科赫建立以下规则,第一行:
- 把一条线段分成三个相等的部分
- 删除的三分之一段的中间
- 中间段替换为两段的长度相同,这样他们都连接
- 重复无限期地在每一个线段
第二幅图显示前两个迭代会是什么样子:18新利最新登入
如果你从一个等边三角形开始,重复这个过程,你最终得到的雪花,有限和无限周边领域:
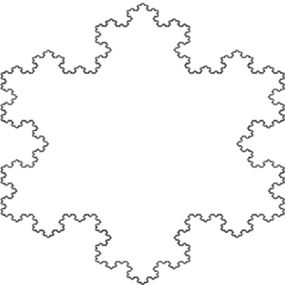
今天,分形形式混乱的视觉识别的一部分。无限复杂的对象在所有尺度自相似,它们代表动力系统在所有的荣耀。事实上曼德布洛特最终证明了洛伦茨吸引子是一个分形,最奇怪的。他们不限于科学家或计算机的渲染的深谋远虑。
分形是在自然界发现的——在海岸线,贝壳、河流、云、雪花和树皮。但是,你实地考察之前,请注意,自相似性表现在自然系统有所不同18新利最新登入。在控制的数学环境中,一个对象和自相似性通常显示一个精确的重复的模式在不同的放大。在自然界中,模式服从统计自相似性,他们不要重复完全相同但部分显示统计特性在不同的尺度。18新利最新登入