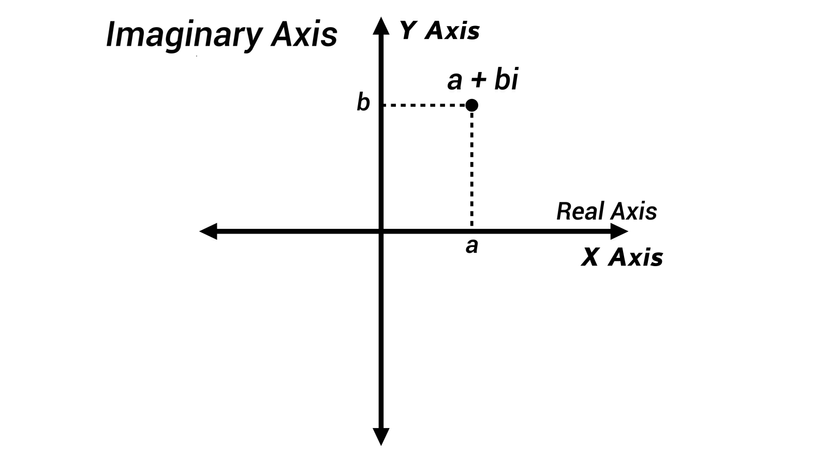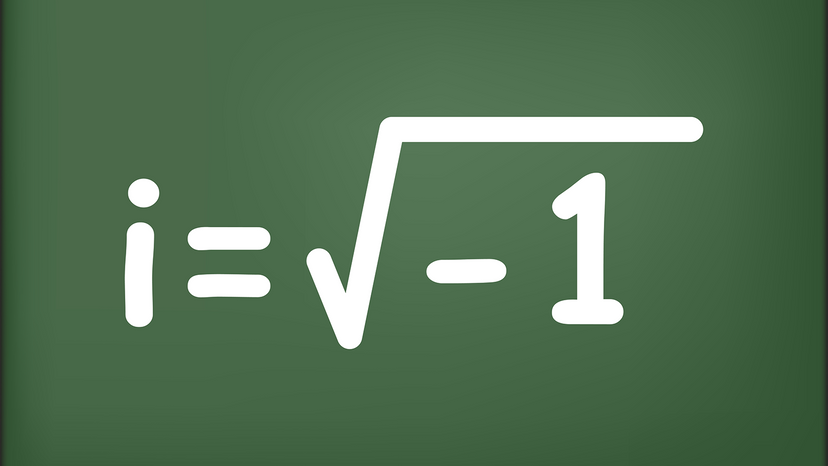
在丹·布朗2003年的超级畅销悬疑惊悚小说中《达芬奇密码》书中主人公罗伯特·兰登和密码学家索菲·奈芙之间有一段妙语连篇的对话,在对话中,索菲·奈芙对“信仰包括奇迹发生在内的信仰的宗教信徒”的价值表示怀疑。看来他们的现实是假的,”她嘲笑道。
兰登笑着说,这些信念并不比“一个数学密码学家相信虚数i,因为它能帮助她破译密码”更虚假。
广告
对于我们这些不懂的人擅长数学兰登的笑话有点令人费解。他说那句话的时候到底在说什么数量是虚构的?18新利最新登入这怎么可能呢?
但事实证明,虚数-基本上,一个数平方后得到一个负数-确实是数学中的一个东西,最早在15世纪和16世纪被发现,用来解决某些令人困惑的方程。虽然最初被认为是一种客厅把戏,但在此后的几个世纪里,它们被视为一种以复杂方式概念化世界的工具,今天在从电气工程到量子力学等领域都很有用。
“我们发明虚数的原因和我们发明负数的原因是一样的,”解释说Cristopher摩尔.他是物理学家圣达菲研究所他与斯蒂芬·默滕斯(Stephan Mertens)合著了2011年出版的《计算的本质."
“从普通算术开始,”摩尔继续说道。“二减七等于几?”如果你从未听说过负数,那就说不通了。没有人接电话。不能有- 5个苹果,对吧?但是这样想。你可以欠我五个苹果,或者五美元。一旦人们开始做会计和簿记,我们就需要这个概念。”同样,今天我们都很熟悉这样的想法:如果我们写了大量的支票来支付东西,但没有足够的钱来支付,我们的银行账户可能会出现负余额。
广告